Какие бывают системы счисления
Позиционные системы счисления
 В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.
Под позиционной системой счисления обычно понимается  -ричная система счисления, которая определяется целым числом
-ричная система счисления, которая определяется целым числом 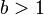 , называемым основанием системы счисления. Целое число без знака
, называемым основанием системы счисления. Целое число без знака  в
в  -ричной системе счисления представляется в виде конечной линейной комбинации степеней числа
-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа  :
:
 -ричная система счисления, которая определяется целым числом
-ричная система счисления, которая определяется целым числом 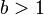 , называемым основанием системы счисления. Целое число без знака
, называемым основанием системы счисления. Целое число без знака  в
в  -ричной системе счисления представляется в виде конечной линейной комбинации степеней числа
-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа  :
: , где
, где  — это целые числа, называемые цифрами, удовлетворяющие неравенству
— это целые числа, называемые цифрами, удовлетворяющие неравенству 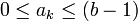 .
.
Каждая степень  в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя
в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя  (номером разряда). Обычно, в ненулевых числах
(номером разряда). Обычно, в ненулевых числах  , левые нули опускаются.
, левые нули опускаются.
 в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя
в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя  (номером разряда). Обычно, в ненулевых числах
(номером разряда). Обычно, в ненулевых числах  , левые нули опускаются.
, левые нули опускаются.
Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число  записывают в виде последовательности его
записывают в виде последовательности его  -ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:
-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:
 записывают в виде последовательности его
записывают в виде последовательности его  -ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:
-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:
Например, число сто три представляется в десятичной системе счисления в виде:
Наиболее употребляемыми в настоящее время позиционными системами являются:
- 2 — двоичная (в дискретной математике, информатике, программировании);
- 3 — троичная;
- 8 — восьмеричная;
- 10 — десятичная (используется повсеместно);
- 12 — двенадцатеричная (счёт дюжинами);
- 13 — тринадцатеричная;
- 16 — шестнадцатеричная (используется в программировании, информатике);
- 60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).
В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.
Смешанные системы счисления
Смешанная система счисления является обобщением  -ричной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел
-ричной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел 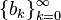 , и каждое число
, и каждое число  в ней представляется как линейная комбинация:
в ней представляется как линейная комбинация:
 -ричной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел
-ричной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел 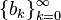 , и каждое число
, и каждое число  в ней представляется как линейная комбинация:
в ней представляется как линейная комбинация: , где на коэффициенты
, где на коэффициенты  , называемые как и прежде цифрами, накладываются некоторые ограничения.
, называемые как и прежде цифрами, накладываются некоторые ограничения.
Записью числа  в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса
в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса  , начиная с первого ненулевого.
, начиная с первого ненулевого.
 в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса
в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса  , начиная с первого ненулевого.
, начиная с первого ненулевого.
В зависимости от вида 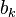 как функции от
как функции от  смешанные системы счисления могут быть степенными, показательными и т. п. Когда
смешанные системы счисления могут быть степенными, показательными и т. п. Когда  для некоторого
для некоторого  , смешанная система счисления совпадает с показательной
, смешанная система счисления совпадает с показательной  -ричной системой счисления.
-ричной системой счисления.
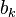 как функции от
как функции от  смешанные системы счисления могут быть степенными, показательными и т. п. Когда
смешанные системы счисления могут быть степенными, показательными и т. п. Когда  для некоторого
для некоторого  , смешанная система счисления совпадает с показательной
, смешанная система счисления совпадает с показательной  -ричной системой счисления.
-ричной системой счисления.
Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд. При этом величина « дней,
дней,  часов,
часов,  минут,
минут,  секунд» соответствует значению
секунд» соответствует значению 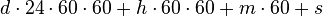 секунд.
секунд.
 дней,
дней,  часов,
часов,  минут,
минут,  секунд» соответствует значению
секунд» соответствует значению 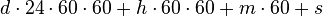 секунд.
секунд.[править]Факториальная система счисления
В факториальной системе счисления основаниями являются последовательность факториалов  , и каждое натуральное число
, и каждое натуральное число  представляется в виде:
представляется в виде:
 , и каждое натуральное число
, и каждое натуральное число  представляется в виде:
представляется в виде: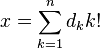 , где
, где  .
.
Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: число, на единицу меньшее номера (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе i! будет обозначать число инверсий для элемента i+1 в том множестве, в котором производятся перестановки (число элементов меньших i+1, но стоящих правее его в искомой перестановке)
[править]Фибоначчиева система счисления
Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число  в ней представляется в виде:
в ней представляется в виде:
 в ней представляется в виде:
в ней представляется в виде: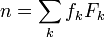 , где
, где  — числа Фибоначчи,
— числа Фибоначчи, 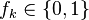 , при этом в коэффициентах
, при этом в коэффициентах 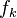 есть конечное количество единиц и не встречаются две единицы подряд.
есть конечное количество единиц и не встречаются две единицы подряд.
[править]Непозиционные системы счисления
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
[править]Биномиальная система счисления
Представление, использующее биномиальные коэффициенты
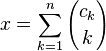 , где
, где  .
.
[править]
[править]Система счисления Штерна–Броко
Система счисления Штерна–Броко — способ записи положительных рациональных чисел, основанный на дереве Штерна–Броко.
[править]Системы счисления разных народов
[править]Единичная система счисления
По-видимому, хронологически первая система счисления каждого народа, овладевшего счётом. Натуральное число изображается путём повторения одного и того же знака (чёрточки или точки). Например, чтобы изобразить число 26, нужно провести 26 чёрточек (или сделать 26 засечек на кости, камне и т.д.). Впоследствии, ради удобства восприятия больших чисел, эти знаки группируются по три или по пять. Затем равнообъёмные группы знаков начинают заменяться каким-либо новым знаком - так возникают прообразы будущих цифр.
[править]Древнеегипетская система счисления
Древнеегипетская десятичная непозиционная система счисления возникла во второй половине третьего тысячелетия до н. э. Для обозначения чисел 0, 1, 10, 10², 10³, 104, 105, 106, 107 использовались специальные цифры. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из цифр повторялась не более девяти раз. Значение числа равно простой сумме значений цифр, участвующих в его записи.[1]
[править]Вавилонская система счисления
[править]Алфавитные системы счисления
Алфавитными системами счисления пользовались древние армяне, грузины, греки (ионическая система счисления), арабы (абджадия), евреи (см. гематрия) и другие народы Ближнего Востока. В славянских богослужебных книгах греческая алфавитная система была переведена на буквы кириллицы.[1]
[править]Еврейская система счисления
Еврейская система счисления в качестве цифр использует 22 буквы еврейского алфавита. Каждая буква имеет своё числовое значение от 1 до 400 (см. т. ж. Гематрия). Ноль отсутствует. Цифры, записанные таким образом, наиболее часто можно встретить в нумерации лет по иудейскому календарю.
[править]
[править]Римская система счисления
Каноническим примером почти непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы:
I обозначает 1,
V — 5,
X — 10,
L — 50,
C — 100,
D — 500,
M — 1000
I обозначает 1,
V — 5,
X — 10,
L — 50,
C — 100,
D — 500,
M — 1000
Например, II = 1 + 1 = 2
здесь символ I обозначает 1 независимо от места в числе.
здесь символ I обозначает 1 независимо от места в числе.
На самом деле, римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из неё, например:
IV = 4, в то время как:
VI = 6
VI = 6
[править]Система счисления майя
Майя использовали 20-ричную систему счисления за одним исключением: во втором разряде было не 20, а 18 ступеней, то есть за числом (17)(19) сразу следовало число (1)(0)(0). Это было сделано для облегчения расчётов календарного цикла, поскольку (1)(0)(0) = 360 примерно равно числу дней в солнечном году.
Для записи основными знаками были точки (единицы) и отрезки (пятёрки).


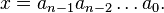
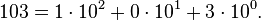
хорошо
ОтветитьУдалить3СВ7 это к какой системе счисления относится?
ОтветитьУдалить